komposisi fungsi dan invers fungsi
nama:shafira putri setiawan
kelas:x mipa 2
KOMPOSISI FUNGSI &
INVERS FUNGSI
Pengertian Fungsi Komposisi
Fungsi komposisi yaitu penggabungan operasi pada dua jenis fungsi f(x) dan g(x) hingga menghasilkan fungsi baru. Operasi fungsi komposisi biasa yaitu dilambangkan dengan “o” dan dibaca dengan komposisi atau bundaran.
Fungsi baru yang bisa terbentuk dari f (x) dan g (x) yaitu:
(fog) (x) = g dimasukkan ke f
(gof) (x) = f dimasukkan ke g
Fungsi tunggal itu merupakan fungsi yang bisa dilambangkan dengan huruf "kabut" atau juga bisa dibaca dengan "fungsi f bundaran g". Fungsi “fog” yaitu fungsi g yang dilakukan terlebih dahulu, lalu f. Sedangkan untuk fungsi “gof” dibaca dengan fungsi g bundaran f. Maka, “gof” yaitu fungsi f terlebih dahulu, lalu g.
Rumus Fungsi Komposisi
Dari rumus tersebut, definisi yang di dapat menyatakan:
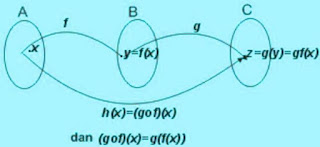
Jika f : A → B ditentukan rumus y = f (x)
Jika g : B → C ditentukan rumus y = g (x)
Jadi, hasil fungsi g dan f:
h (x) = ( g o f ) (x) = g ( f (x))
Dari penjelasan tersebut bisa dikatakan bahwa fungsi yang melibatkan fungsi f dan g bisa ditulis:
(gof) (x) = g (f (x)
Contoh :
Diberikan dua buah fungsi yang masing-masing f (x) dan g (x) berturut-turut yaitu:
f (x) = 3x + 2 dan g (x) = 2 - x
Tentukanlah:
a) ( f o g ) (x) &
b) ( g o f ) (x)
Data Jawaban :
f (x) = 3x + 2
g (x) = 2 - x
a) ( f o g ) (x)
“Masukkanlah g (x) nya ke f (x)”
hingga menjadi:
( f o g ) (x) = f ( g (x))
= f (2 - x)
= 3 (2 - x) + 2
= 6 - 3x + 2
= - 3x + 8
b) ( g o f ) (x)
“Masukkanlah f (x) nya ke g (x)”
Hingga menjadi:
( f o g ) (x) = g ( f (x))
= g (3x + 2)
= 2 - (3x + 2)
= 2 - 3x - 2
= - 3x
Fungsi Invers
Pengertian dan Contoh Soal Fungsi Invers
Dalam fungsi biasanya untuk menentukan nilai atau petanya maka kita masukan nilai domain ke rumus fungsi dan kemudian kita akan mendapatkan petanya. Hal sebaliknya dapat kita lakukan yaitu dari peta kita akan mendapatkan domainnya. Kita dapat melakukanya dengan memasukkan petanya ke fungsi inversnya. Pada bahasan kali ini, akan dibahas mengenai Fungsi Invers baik itu, pengertian, sifat-sifat dan contoh soalnya. Namun, untuk mempermudah memahami materi ini, syaratnya adalah anda harus memahami terlebih dahulu mengenai relasi dan fungsi.
Pengertian Fungsi Invers
Fungsi Invers atau dapat disebut sebagai Fungsi Kebalikan adalah fungsi yang merupakan kebalikan dari aksi fungsi awalnya. Setiap fungsi mempunyai invers, namun setiap invers belum tentu sebuah fungsi. Ini berarti invers dari suatu fungsi dapat berupa relasi atau fungsi. Untuk lebih memahaminya, simaklah penjelasan berikut.
Misalkan terdapat dua fungsi yaitu fungsi f dan g yang digambarkan dalam diagram panah di bawah ini.
Apabila fungsi g dan f dibalik maka akan menghasilkan R1 dan R2. R1 merupakan invers dari fungsi g yang bukan fungsi dan termasuk ke dalam relasi. Karena ada anggota B yang tidak memiliki pasangan di A serta terdapat anggota yang memiliki pasangan lebih dari satu, sehingga R1 bukan fungsi. Sedangkan R2 merupakan invers dari fungsi g yang termasuk fungsi. Karena setiap anggota B memiliki tepat satu pasangan di A. Dengan demikian R2 dapat dikatakan sebagai fungsi invers dari f yang biasanya dinotasikan dengan f−1
Syarat Invers Fungsi Dikatakan Fungsi
Fungsi infers dari f dinyatakan dengan menambahkan "−1" pada f atau ditulis f−1 . Dari penjelasan sebelumnya, terlihat bahwa f−1 ada apabila f dalam keadaan berkorespondensi satu-satu atau f adalah fungsi bijektif. Perhatikan diagram fungsi f di bawah
Menetukan Fungsi Invers Suatu Fungsi
Untuk menentukan fungsi invers dari suatu fungsi dapat dilakukan dengan cara berikut ini.
• Buatlah pemisalan f(x) = y pada persamaan
• Persamaan tersebut disesuaikan dengan f(x) = y, sehingga ditemukan fungsi dalam y dan nyatakanlah x = f(y)
• Gantilah y dengan x, sehingga f(y) = f-1(x)




Komentar
Posting Komentar